Like any other physical theory, quantum mechanics tries to establish correlations between some given initial conditions and the results of subsequent measurements.
Quantum correlations are inherently statistical. If a measurement is repeated several times in identical conditions, one doesn't get the same result at each repetition. Therefore, in general, one cannot predict with certainty the result of a single observation (see uncertainty.)
The fundamental implications of the superposition principle have been intensely debated. If, at odds with the instrumentalist view, quantum states are supposed to describe a real state of affairs (and not merely to predict possible occurrences), then a number of paradoxes (like the one of Schrödinger's cat) and fundamental difficulties (like the ‘measurement problem') arise (see implications).
New research fields have been implemented to study the practical consequences of the superposition principle. An important issue that is currently being addressed, both theoretically and experimentally, is how to manipulate the quantum information encoded in the so-called entangled states (see implications) .
A distinctive feature of quantum probability distributions is that they display wavelike patterns and obey the uncertainty relations.
The formal tool allowing one to deal with quantum probabilities are the so-called quantum states. According to the instrumentalist view, first advocated by Max Born and the Copenhagen School, quantum states do not represent any real physical properties or ensemble of properties belonging to a system; they merely provide the information necessary to draw all sorts of statistical predictions about results obtained in a well-specified experimental context (see origins).
Quantum states are usually represented by vectors belonging to a particular vector space called a Hilbert space. The representation of states in the Hilbert space is closely related to the principle of superposition.
However, the probability of getting a given result is reproducible and can be anticipated (this can be verified by comparing the statistical frequency of each outcome in different series of repetitions.) The probabilities p(a1)..… p(an) associated with the possible values a1.....an of an observable A, form a probability distribution (provided that p(a1) + p(a2) + … + p(an) = 1).
Probability distributions are of course employed in classical physics too. But there, the use of probability is supposed to reflect our contingent ignorance about facts that are relevant to supply a complete description of what is going on. For example, we lack an infinitely accurate knowledge of the initial conditions, and this prevents us from drawing deterministic predictions (i.e. predictions assigning probability 0 to all the outcomes but one). But even if not itself deterministic, the structure of the correlations observed in classical physics is nonetheless compatible (to a certain extent) with the assumption of ‘underlying' determinism - i.e. the assumption that the observed phenomena arise from a deterministic chain of events. This bare assumption turns out instead to be untenable in quantum mechanics (see implications and uncertainty for further discussion).
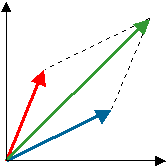
This principle, first formulated by P.A.M. Dirac, asserts that if two quantum states correspond to physically realisable situations, then also does their superposition. The term ‘superposition' refers here to the linear combination of two vectors (given two vectors 
and 
, a linear combination of the two is the vector: 
, where 
are two arbitrary numbers). The principle of superposition is a way to say that, in order to correctly anticipate the correlations observed in the quantum world, we need all the vectors belonging to the Hilbert space.
State vectors provide a very general and powerful predictive structure, covering both deterministic and indeterministic models (see origins). Quantum particles displaying wavelike patterns, for example, are readily represented in the state space (this is not too surprising, since waves, like vectors, obey a superposition principle).