‘It seems to be a general law of nature that we cannot determine position and velocity simultaneously with arbitrary accuracy'. This is the ‘uncertainty principle', as originally stated by Werner Heisenberg in 1927. Mathematically, it takes the form of an inequality that applies to the ‘uncertainties' affecting position and momentum (the momentum of a body is the product of its mass and velocity). Since position and momentum are vectors, one has to consider separately their orthogonal components. For position and momentum along the x-axis, the uncertainty relation writes for example:

Analogous inequalities hold for the y and z components. For all these pairs of variables, the Planck's constant h sets an absolute lower bound to the product of the relative uncertainties. But what exactly are ‘uncertainties'?

Notice however that inequality (1) does not place a limit on the precision to which the value of a single variable can be predicted. The experimental arrangement can be conceived so as to make the uncertainty Dx on the position arbitrarily small. But then the uncertainty Dp_x on the momentum will be large enough for the product DxDp_x to overcome h/4p. Thus, according to quantum mechanics, to predict with great accuracy the value of the position, we must give up the possibility of predicting the exact value of the velocity, and vice versa.

One may wonder why, when dealing with macroscopic bodies, we don't have to face such a limitation. To understand this point, we must take into account the fact that, in practice, the accuracy of measurements is affected by the finite resolution of real instruments. Since the Planck's constant is very small, when large mass objects are involved, the spreads due to experimental limitations are generally much larger than the fundamental uncertainties derived from (1). The effects of the Heisenberg's principle are thus masked by other limitations that are preponderant at the macroscopic scale.

The uncertainty relations are not restricted to position and velocity. They apply more generally to any pair of quantities that are in some sense ‘complementary'. In particular, they set a limit on the simultaneous determination of time and energy variables. The time/energy uncertainty relations are connected to several interesting phenomena (see implications).

Quantum observables may occasionally take a value that is quite far from the mean expectation. These occurrences are called quantum fluctuations. Energy fluctuations of quantum vacuum are responsible for the physical effects attributed to the so-called virtual particles. Virtual particles appear out of vacuum only to disappear in times less than the limits set by the uncertainty relations. Fluctuations living for a very short time can be as energetic as to produce pairs of massive particles (this is a consequence of the equivalence of energy and mass.) The notion of virtual particle is helpful to visualize elementary processes (virtual particles are said to mediate the interactions between elementary particles, just as ‘real' bosons do).

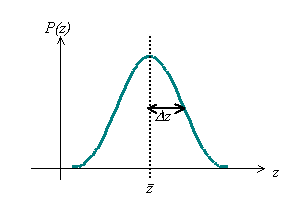
Let's consider first a non-quantum example: a stone, initially at rest, is dropped from the top of a tower and its vertical position and momentum are recorded after a given delay. The experiment is repeated several times. Provided that the time elapsed between the drop and the measurement is the same in each repetition, we always get the same values for z and p_z (namely, the values predicted by classical mechanics). Now we perform the same kind of experiment on the atomic scale. In this (quantum) case, what we find is that, regardless of the accuracy of the experiment, the measured values for z and p_z vary from one repetition to another. The results obtained for z and p_z are fitted by a bell distribution centred on a mean value. (This is what happens in classical physics when the initial conditions are not well controlled or the measurement is not precise.) The ‘uncertainties' Dz and Dp_z tell us how large these distributions are, or, in other words, how far from the average values of z and p_z we can expect to find an individual outcome. Indeed, quantum predictions are intrinsically probabilistic (see superpositions): as far as we deal with a single repetition of the experiment, all we know in advance is that the measured value for, say, z, is likely to lie somewhere within the range of values Dz centred around the average value (see picture).